[알고리즘] 최소 신장 트리(Minimum Spanning Tree)

최소 신장 트리(Minimum Spanning Tree)

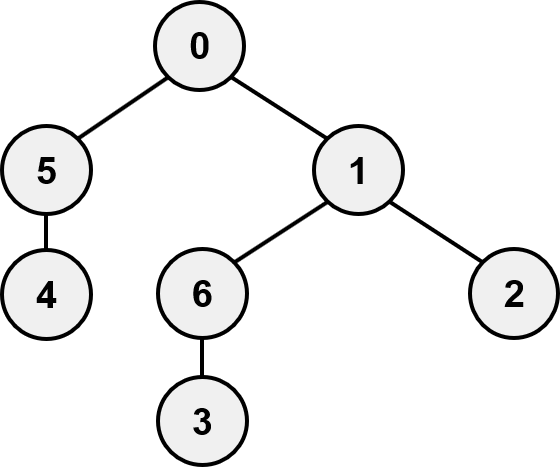
신장 트리(Spanning Tree)는 그래프 내에 있는 모든 정점을 연결하고 사이클이 없는 그래프를 의미합니다. n개의 정점이 있다면 신장 트리의 간선 수는 n-1개가 됩니다. 최소 신장 트리는 각 간선이 가지고 있는 가중치의 합이 최소가 되는 신장 트리입니다. 가중치는 거리, 비용, 시간 등 여러가지로 응용할 수 있습니다. 최소 신장 트리의 대표적인 알고리즘으로는 프림 알고리즘(Prim’s Algorithm)과 크루스칼 알고리즘(Kruskal’s Algorithm)이 있습니다.

프림 알고리즘(Prim’s Algorithm)

프림 알고리즘은 로버트 프림(Robert C. Prim)이 만든 최소 신장 트리 알고리즘 입니다. 프림 알고리즘은 최소 신장 트리에 연결된 정점 주변에 있는 간선의 가중치 중 가장 작은 것을 골라 최소 신장 트리를 만드는 방법입니다. 프림 알고리즘으로 최소 신장 트리를 만드는 방법은 다음과 같습니다.

1. 그래프와 비어 있는 최소 신장 트리를 만듦
2. 임의의 정점을 시작 정점으로 선택하고 최소 신장 트리의 루트 노드로 삽입
3. 최소 신장 트리에 삽입된 정점과 이 정점과 인접한 정점의 가중치를 확인해서 가장 작은 가중치를 최소 신장 트리에 삽입. (최소 신장 트리에 삽입 시 사이클이 형성되지 않게 삽입)
4. 3번 과정을 반복 한 후 모든 정점이 최소 신장 트리에 연결되면 종료

이해를 돕기 위해 예를 들어 보겠습니다.

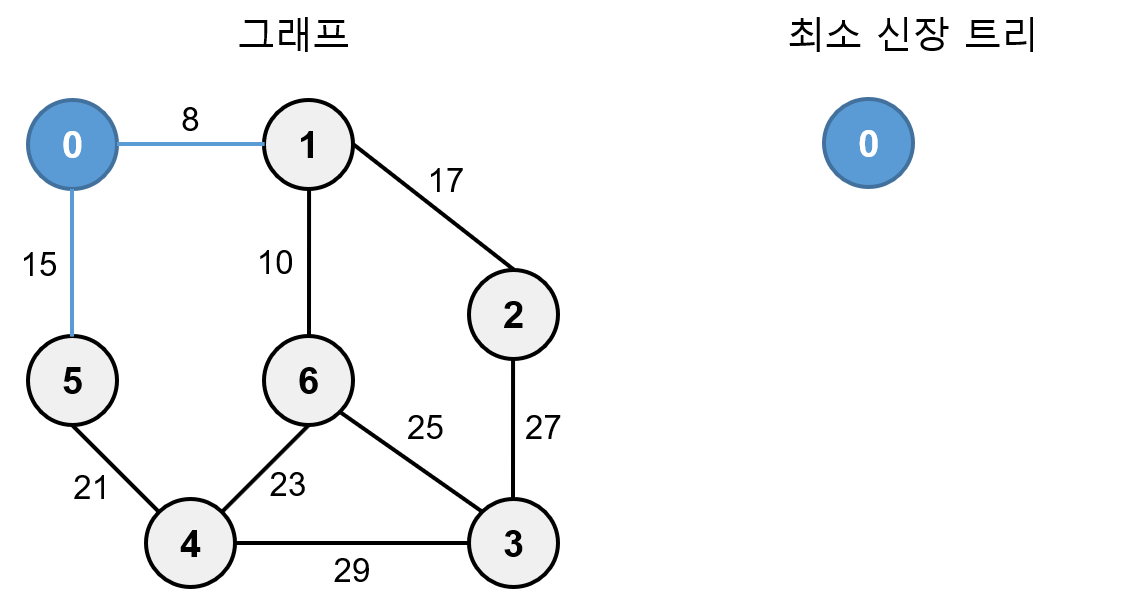
위 그래프에서 정점 0 부터 시작해서 하겠습니다. 정점 0 을 최소 신장 트리에 추가합니다. (파란색 선은 인접한 간선을 의미합니다.)
0에 연결되어 있는 간선 0-1, 0-5 중 가중치가 가장 작은 간선은 가중치가 8인 0-1 이므로 1을 최소 신장 트리에 추가합니다.

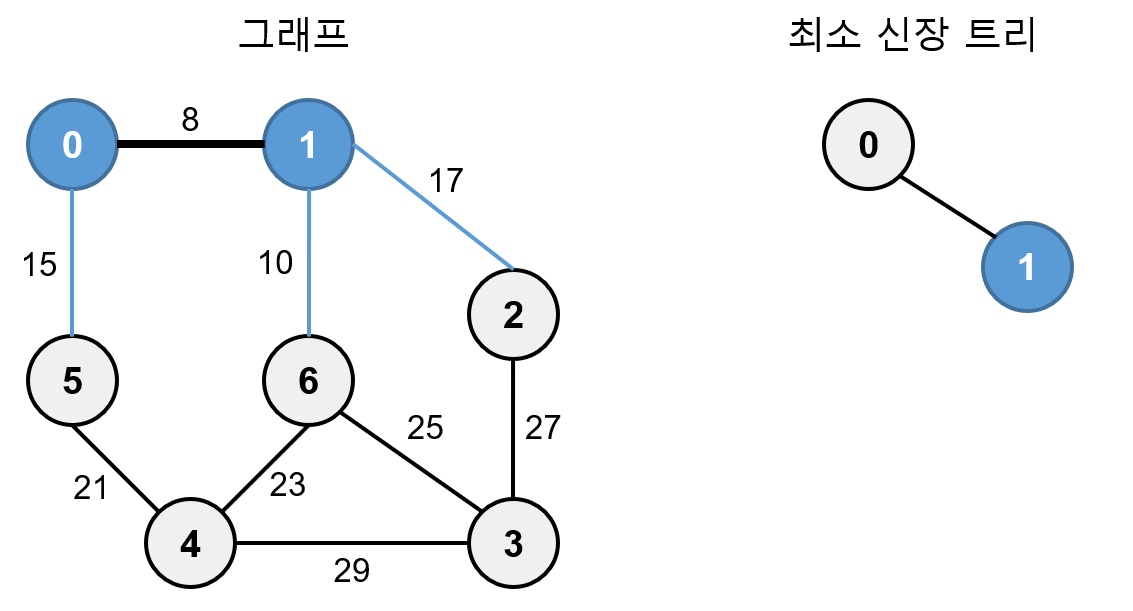
0, 1에 연결되어 있는 간선 0-5, 1-2, 1-6 중 가중치가 가장 작은 간선은 가중치가 10인 1-6 이므로 6을 최소 신장 트리에 추가합니다.

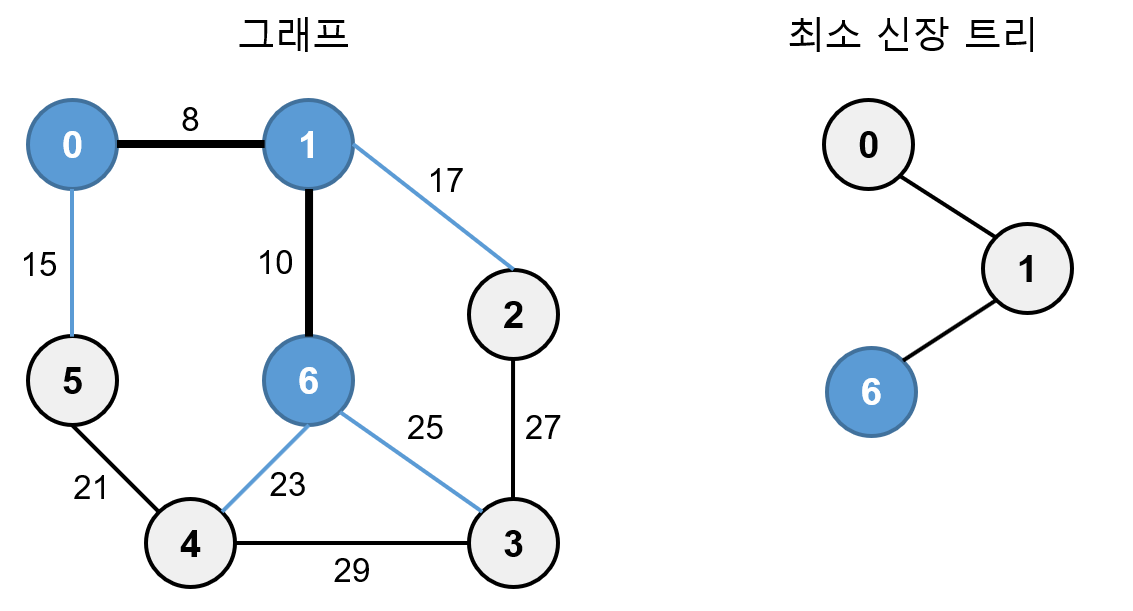
0, 1, 6에 연결되어 있는 간선 0-5, 1-2, 6-3, 6-4 중 가중치가 가장 작은 간선은 가중치가 15인 0-5 이므로 5를 최소 신장 트리에 추가합니다.

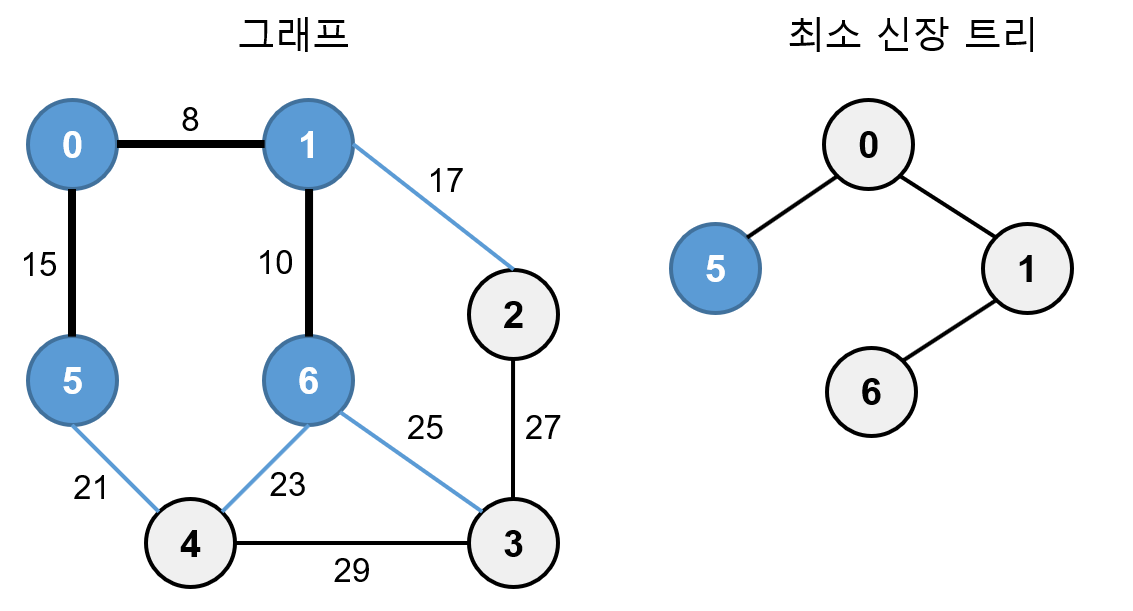
0, 1, 5, 6에 연결되어 있는 간선 1-2, 5-4, 6-3, 6-4 중 가중치가 가장 작은 간선은 가중치가 17인 1-2 이므로 2를 최소 신장 트리에 추가합니다.

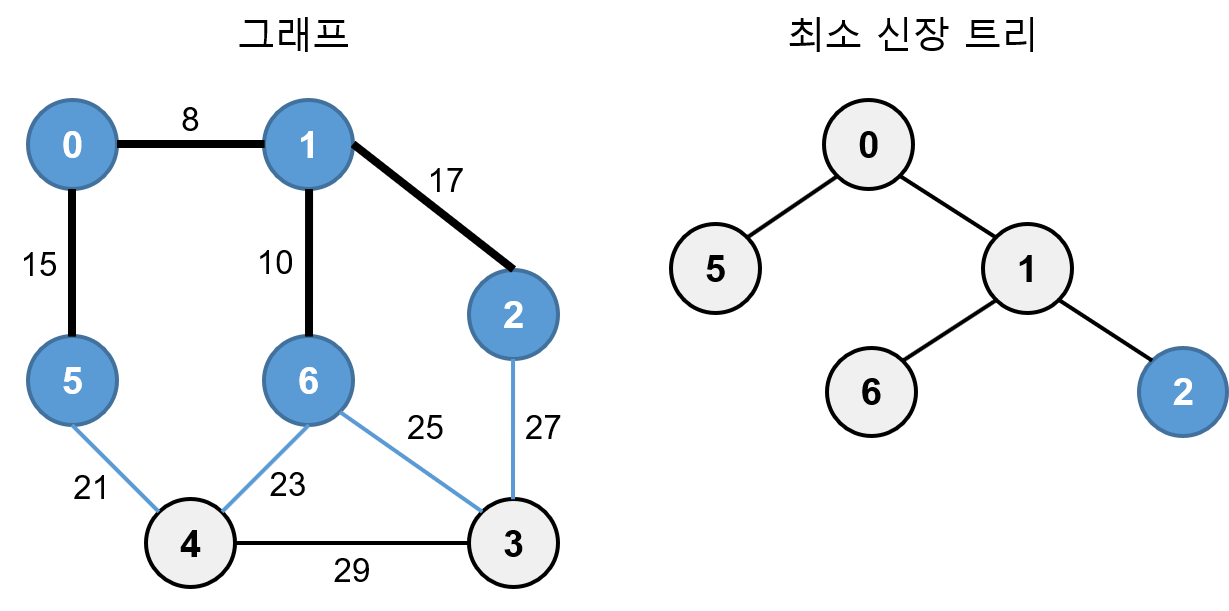
0, 1, 2, 5, 6에 연결되어 있는 간선 2-3, 5-4, 6-3, 6-4 중 가중치가 가장 작은 간선은 가중치가 21인 5-4 이므로 4를 최소 신장 트리에 추가합니다.

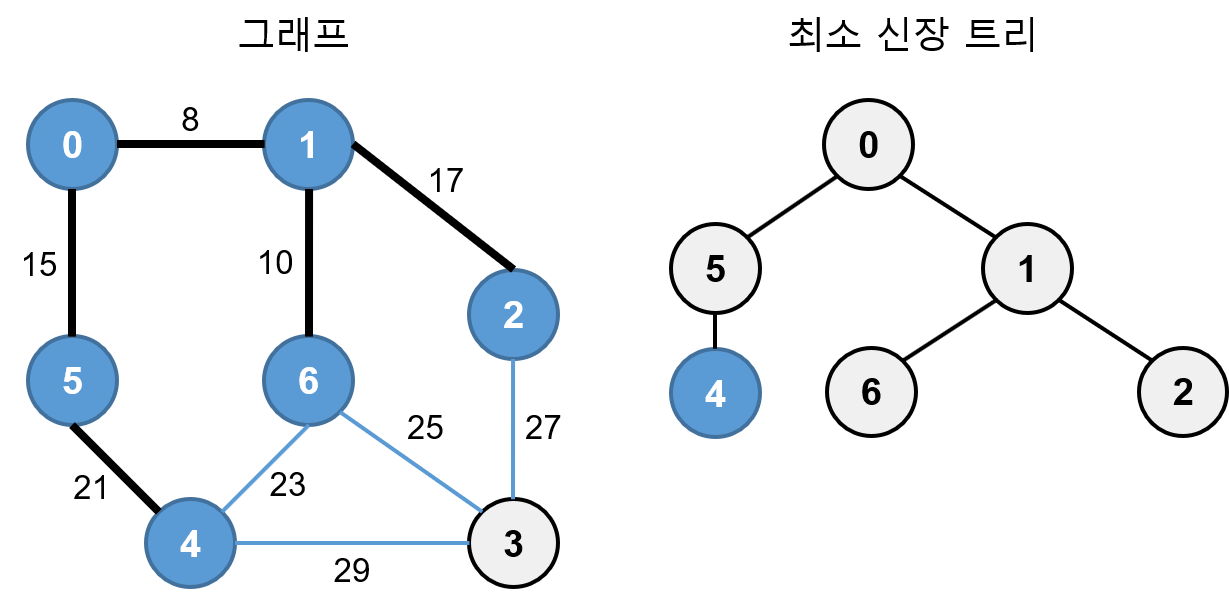
0, 1, 2, 4, 5, 6에 연결되어 있는 간선 2-3, 4-3, 6-3, 6-4 중 가중치가 가장 작은 간선은 가중치가 23인 6-4이지만 6-4를 선택하면 사이클이 형성 되므로 최소 신장 트리에 추가하지 않고, 23 다음으로 작은 가중치가 25인 3을 최소 신장 트리에 추가합니다.

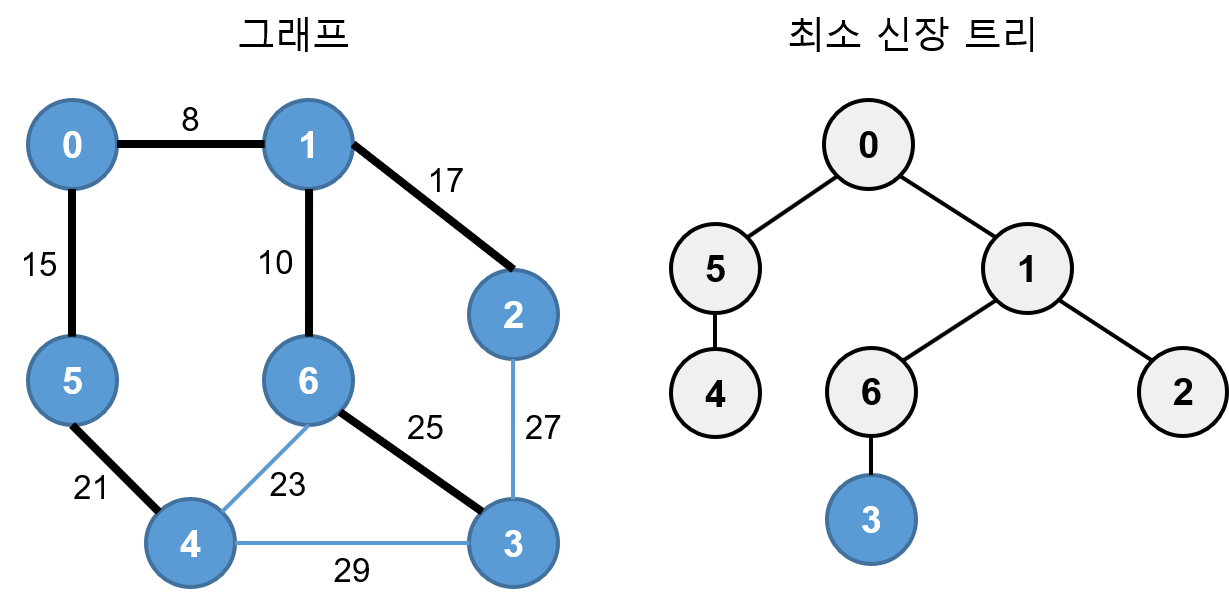
모든 정점이 최소 신장 트리에 추가되었으므로 종료합니다.

프림 알고리즘 구현

프림 알고리즘에서 문제가 되는 것은 최소 가중치를 찾는 것입니다.

그래프에서 N개의 정점이 있다면, N개의 정점을 추가하고 N개의 정점을 순회해야 하므로, 최소 가중치를 찾기 위해서는 N×N=N^2 을 반복해야 합니다.
이 문제를 해결하기 위해서는 힙(Heap)을 사용합니다. 힙을 사용하면 빠르게 최소 가중치를 찾을 수 있습니다.

최소 신장 트리에서 정점과 인접한 간선을 (가중치, 정점)으로 힙에 삽입하고, 힙에서 꺼낸 정점과 인접한 정점을 순회하면서 가중치가 최소인 정점을 다시 힙에 추가하면서 힙이 비어 있을 때까지 반복합니다. 사이클 형성 방지를 위해 이미 방문한 정점일 경우 최소 신장 트리에 추가하지 않습니다.

예제 코드에서는 최소 신장 트리를 반환하게 코드를 작성했습니다. 최소 가중치의 합을 반환하는 등 다양하게 응용하면 될 것 같습니다. 다음은 프림 알고리즘을 구현한 예제 코드입니다.

import sys
import heapq

def prim(start, graphs, weights):
    mst_graphs = [ [ 0 for _ in range(len(graphs)) ] for _ in range(len(graphs)) ] # 최소 신장 트리
    mst_vertices = [-1 for _ in range(len(graphs))] # 최소 신장 트리 연결 정보 (-1로 초기화)
    mst_weights = [ sys.maxsize for _ in range(len(graphs)) ] # 최소 신장 트리 가중치 정보 (최대 값으로 초기화)
    visited = set() # 방문 정보
    heap = [] # 최소 힙

    heapq.heappush(heap, (0, start)) # (가중치, 정점) 쌍으로 힙에 저장

    while len(heap) > 0:
        vertex = heapq.heappop(heap)[1] # 힙에서 최소 가중치 꺼냄
        visited.add(vertex)

        for target, value in enumerate (graphs[vertex]): # 인접한 간선 순회
            if target in visited:
                continue    

            if value == 1 and weights[vertex][target] < mst_weights[target]:
                heapq.heappush(heap, (weights[vertex][target], target))
                mst_weights[target] = weights[vertex][target]
                mst_vertices[target] = vertex

    # 최소 신장 트리 생성
    weight_sum = 0
    for a, b in enumerate(mst_vertices):
        if b >= 0:
            mst_graphs[a][b] = 1
            mst_graphs[b][a] = 1
            weight_sum += mst_weights[a]

    # 출력용
    print("최소 가중치 합: ", weight_sum)
    for row in mst_graphs:
        print(row)

    return mst_graphs

if __name__ == "__main__":
    graphs = [
        [0, 1, 0, 0, 0, 1, 0],
        [1, 0, 1, 0, 0, 0, 1],
        [0, 1, 0, 1, 0, 0, 0],
        [0, 0, 1, 0, 1, 0, 1],
        [0, 0, 0, 1, 0, 1, 1],
        [1, 0, 0, 0, 1, 0, 0],
        [0, 1, 0, 1, 1, 0, 0],
        ]
    weights = [
        [0, 8, 0, 0, 0, 15, 0],
        [8, 0, 17, 0, 0, 0, 10],
        [0, 17, 0, 27, 0, 0, 0],
        [0, 0, 27, 0, 29, 0, 25],
        [0, 0, 0, 29, 0, 21, 23],
        [15, 0, 0, 0, 21, 0, 0],
        [0, 10, 0, 25, 23, 0, 0],
        ]

    mst_graphs = prim(0, graphs, weights)

최소 가중치 합:  96
[0, 1, 0, 0, 0, 1, 0]
[1, 0, 1, 0, 0, 0, 1]
[0, 1, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 1]
[0, 0, 0, 0, 0, 1, 0]
[1, 0, 0, 0, 1, 0, 0]
[0, 1, 0, 1, 0, 0, 0]

크루스칼 알고리즘(Kruskal’s Algorithm)

크루스칼 알고리즘은 그래프 내의 모든 간선의 가중치를 확인하고 가장 작은 가중치부터 확인해서 최소 신장 트리를 만드는 방법입니다. 크루스칼 알고리즘은 탐욕적인(Greedy) 방법을 사용합니다.

크루스칼 알고리즘으로 최소 신장 트리를 만드는 방법은 다음과 같습니다.

1. 그래프 내의 모든 간선의 가중치를 오름차순으로 정렬
2. 오름차순으로 정렬된 가중치를 순회하면서 최소 신장 트리에 삽입 (최소 신장 트리에 삽입 시 사이클이 형성되지 않게 삽입)

크루스칼 알고리즘에서 사이클을 확인하기 위해 분리 집합(Disjoint Set)을 사용합니다. 분리 집합은 다음과 같이 서로 공통된 원소를 갖지 않는 집합을 의미합니다.

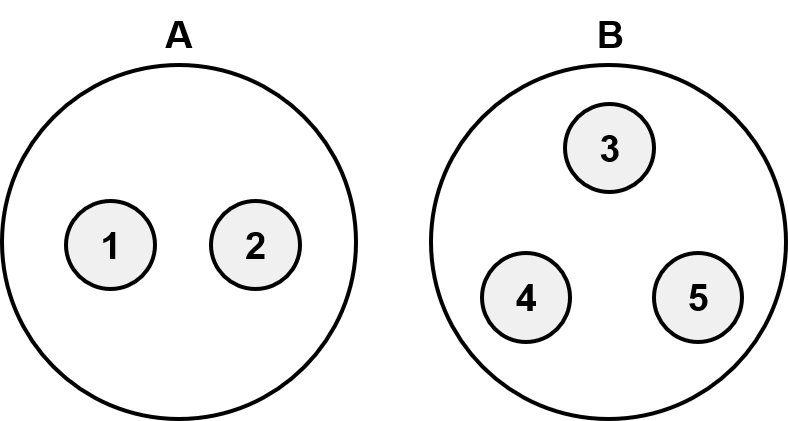
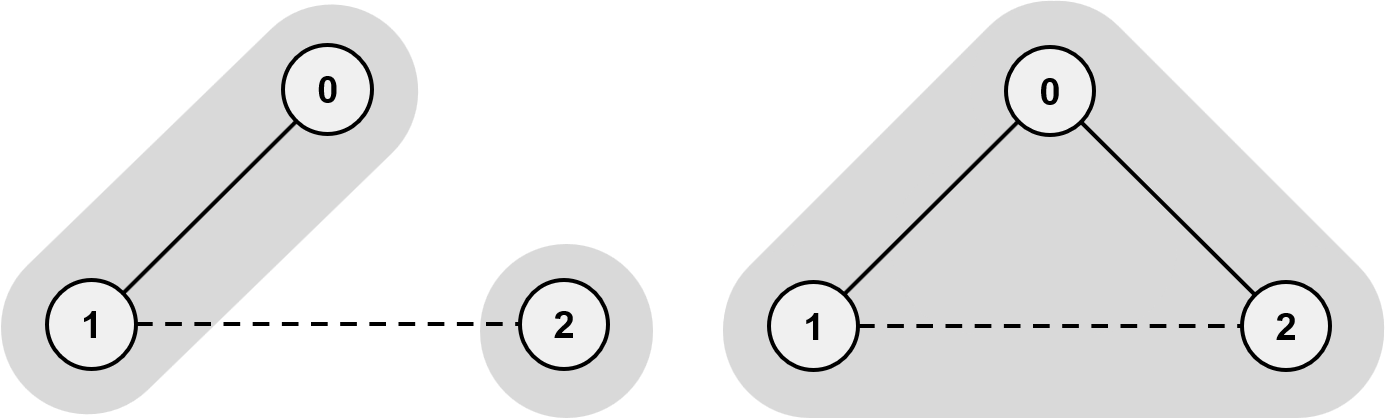
최소 신장 트리에서 다음과 같은 집합이 있고 1-2를 간선으로 연결할 경우, 왼쪽은 서로 다른 집합이기 때문에 1-2를 연결해도 사이클이 형성 되지 않지만, 오른쪽은 이미 같은 집합에 속해 있기 때문에 1-2를 연결할 경우 사이클을 형성하게 됩니다. 이렇게 하면 쉽게 사이클을 확인할 수 있습니다.

이해를 돕기 위해 프림 알고리즘에서 사용했던 예제와 동일한 그래프로 예를 들어 보겠습니다.

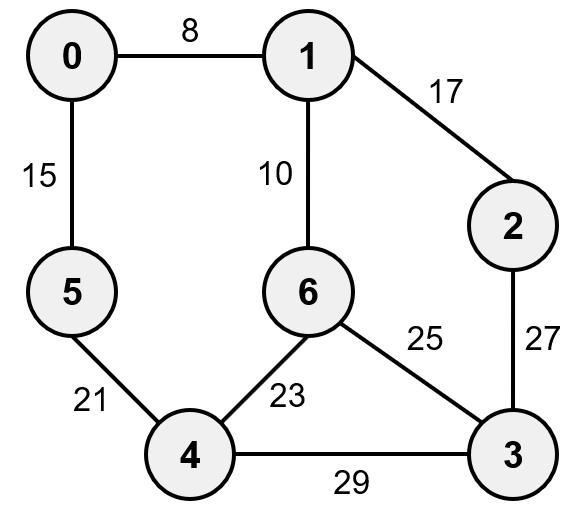
먼저 그래프 내의 모든 간선을 가중치를 기준으로 오름차순으로 정렬한 후, 각 정점 별로 분리 집합을 만듭니다.

간선	가중치
0-1	8
1-6	10
0-5	15
1-2	17
4-5	21
4-6	23
3-6	25
2-3	27
3-4	29

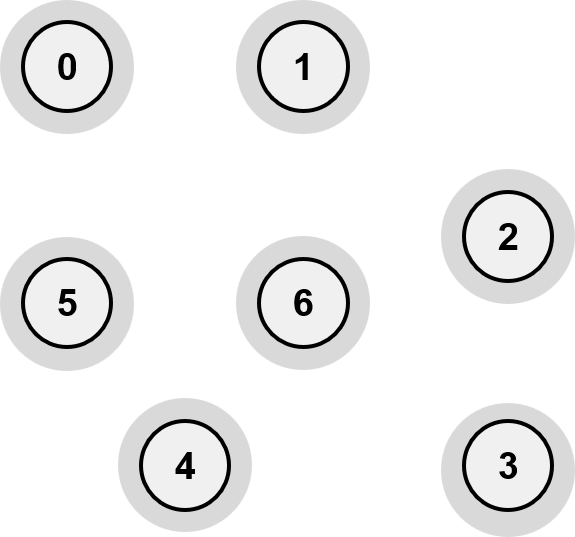
첫번째로 정렬된 가중치가 8인 0-1은 서로 다른 집합이므로 최소 신장 트리에 추가하고 간선으로 연결합니다. 그리고 집합 {0}, {1}을 합집합 연산을 해서 하나의 분리 집합으로 만듭니다.

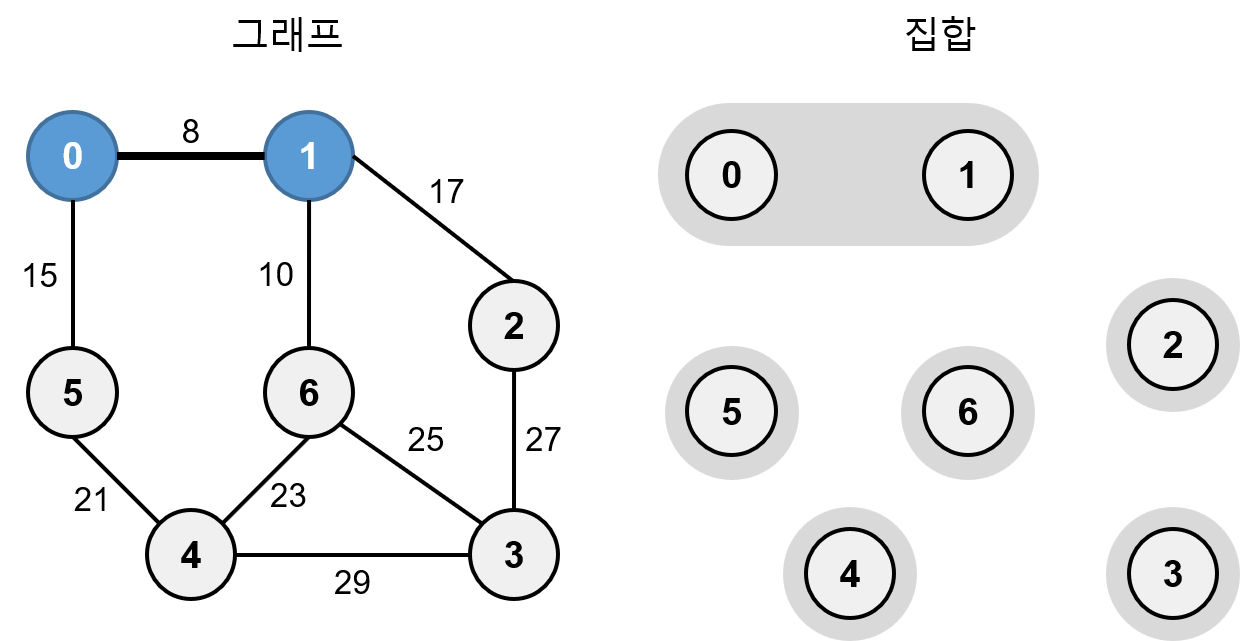
다음으로 가중치가 10인 1-6은 서로 다른 집합이므로 최소 신장 트리에 추가하고 간선으로 연결합니다. 그리고 집합 {0, 1}, {6}을 합집합 연산을 해서 하나의 분리 집합으로 만듭니다.

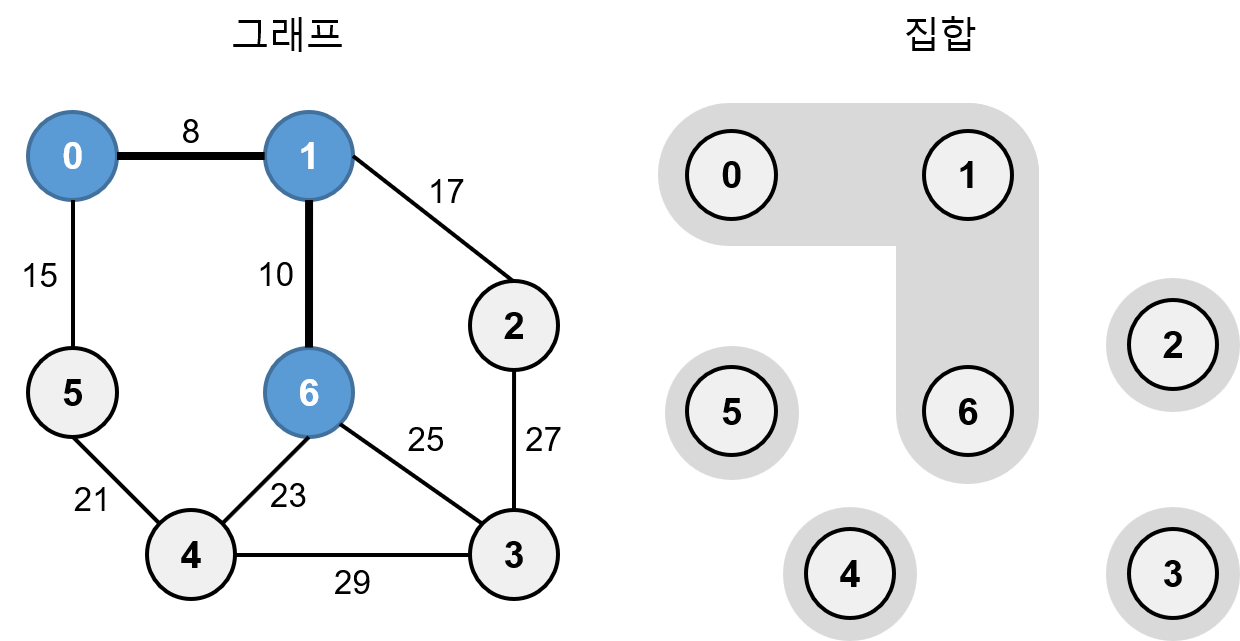
가중치가 15인 0-5는 서로 다른 집합이므로 최소 신장 트리에 추가하고 간선으로 연결합니다. 그리고 집합 {0, 1, 6}, {5}을 합집합 연산을 해서 하나의 분리 집합으로 만듭니다.

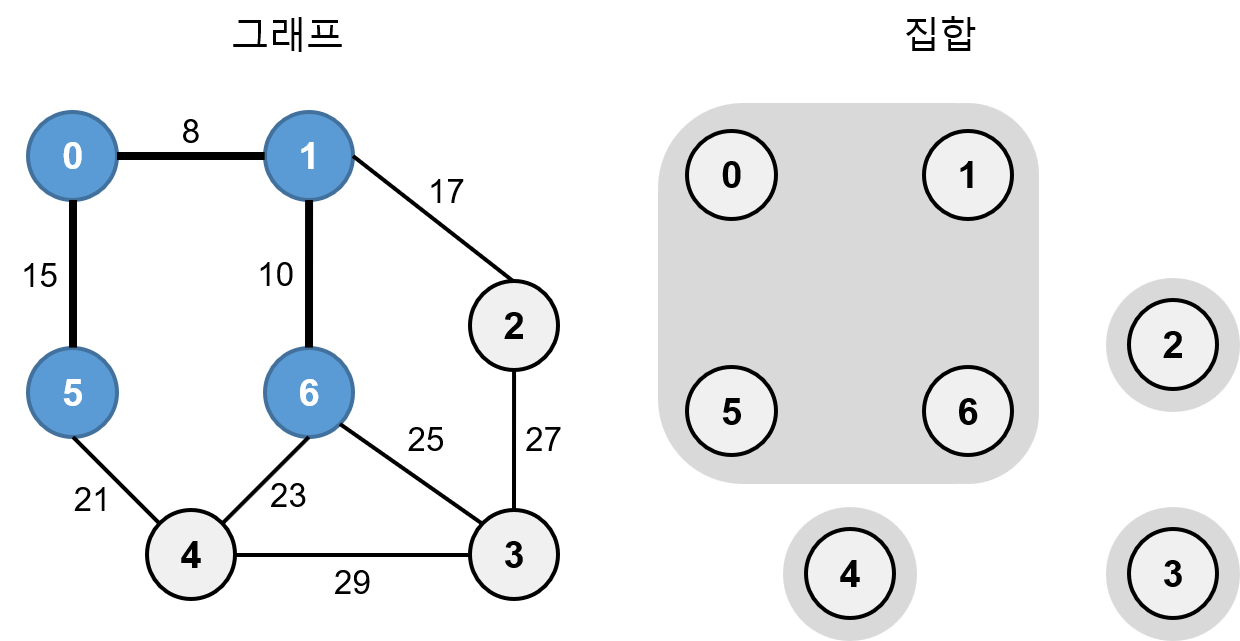
가중치가 17인 1-2는 서로 다른 집합이므로 최소 신장 트리에 추가하고 간선으로 연결합니다. 그리고 집합 {0, 1, 5, 6}, {7}을 합집합 연산을 해서 하나의 분리 집합으로 만듭니다.

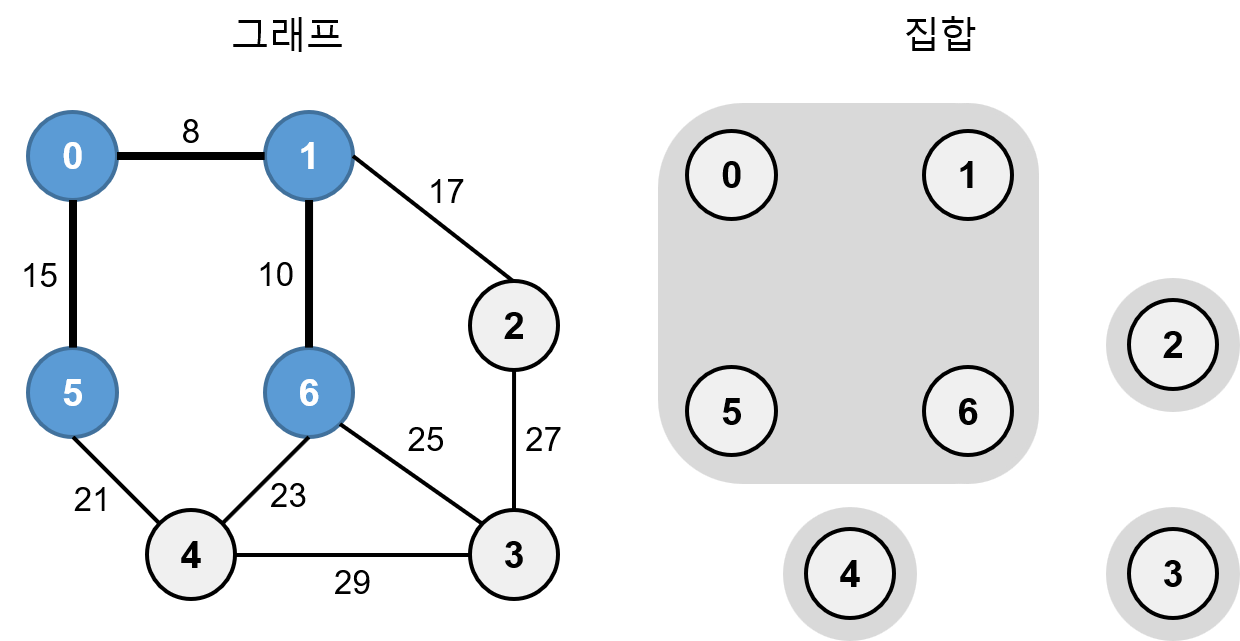
가중치가 21인 4-5는 서로 다른 집합이므로 최소 신장 트리에 추가하고 간선으로 연결합니다. 그리고 집합 {0, 1, 2, 5, 6}, {4}을 합집합 연산을 해서 하나의 분리 집합으로 만듭니다.

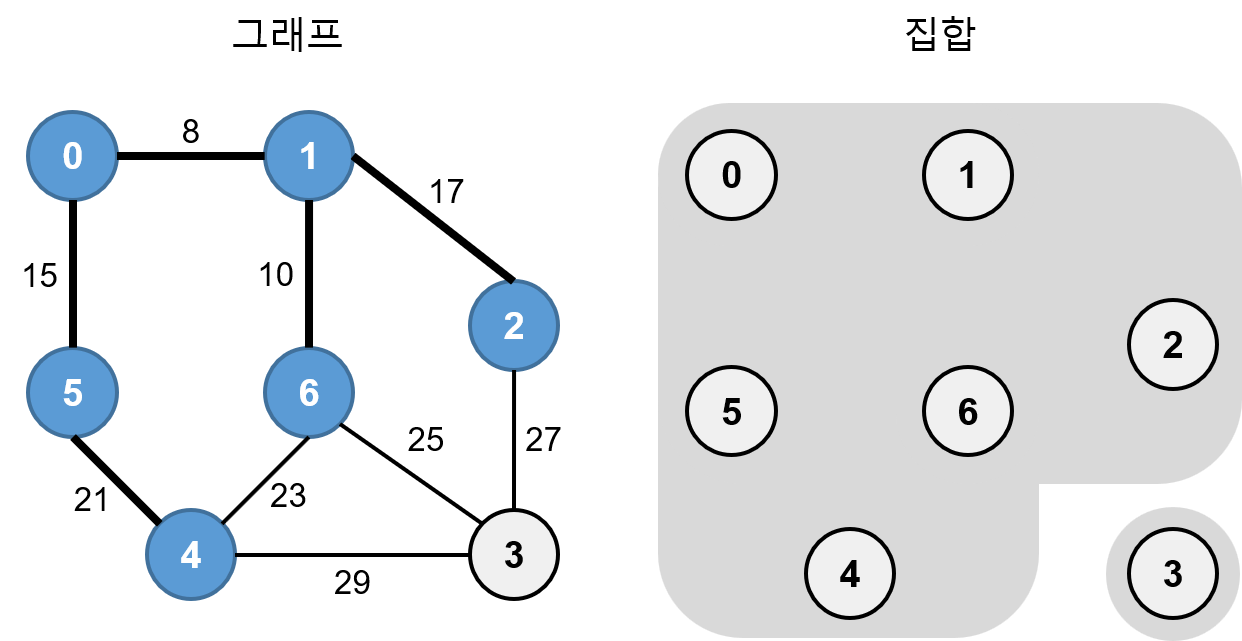
가중치가 23인 4-6은 서로 같은 집합에 속해 있으므로 간선을 연결하면 사이클을 형성합니다. 따라서 다음 가중치를 확인합니다.

가중치가 25인 3-6은 서로 다른 집합이므로 최소 신장 트리에 추가하고 간선으로 연결합니다. 그리고 집합 {0, 1, 4, 5, 6}, {3}을 합집합 연산을 해서 하나의 분리 집합으로 만듭니다.

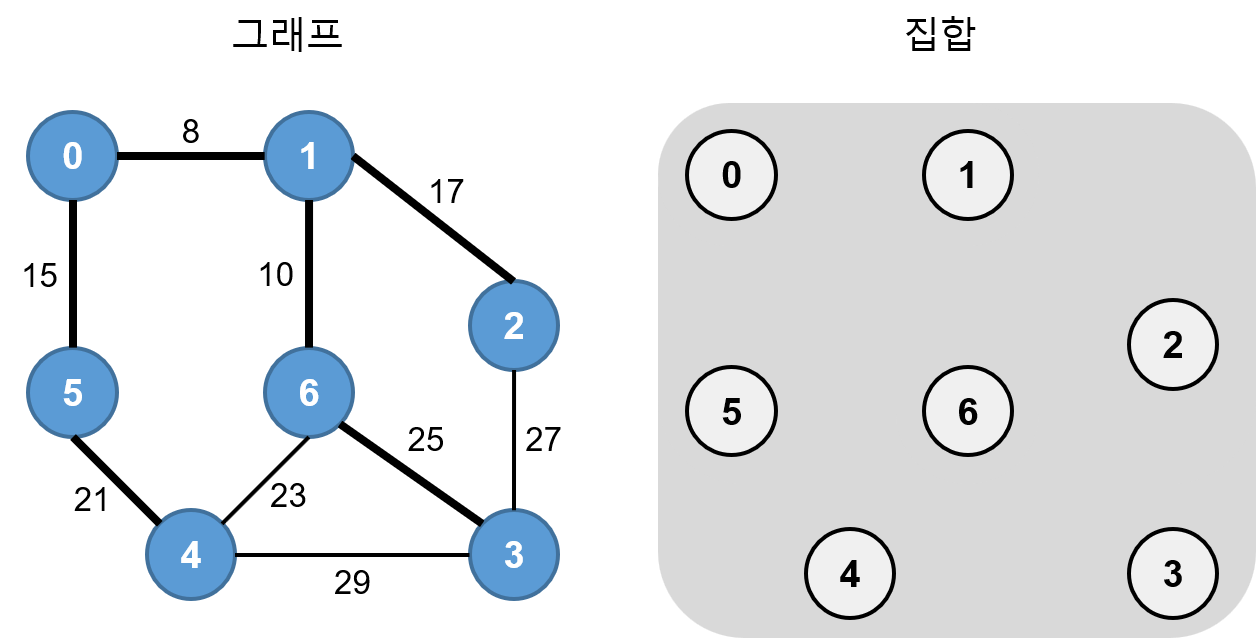
모든 정점이 하나의 집합 안에 포함되었으므로 최소 신장 트리가 만들어졌습니다. 남은 가중치를 확인해보면 모두 사이클을 형성하므로 더 이상 최소 신장 트리에 추가되지 않습니다.

크루스칼 알고리즘 구현

그래프 내의 모든 간선의 가중치를 (가중치, 정점, 정점) 쌍으로 힙에 삽입하고, 힙에서 데이터를 꺼내면서 정점1, 정점2가 서로 다른 집합이면 최소 신장 트리를 생성하고 합집합 연산을 수행합니다. 이 과정을 힙이 비어 있을 때까지 반복합니다. 또한 사이클을 확인하기 위해 분리 집합 클래스, 분리 집합 부모 찾기, 합집합 연산 함수를 구현하였습니다.

예제 코드에서는 프림 알고리즘과 마찬가지로 최소 신장 트리를 반환하게 코드를 작성했습니다. 다음은 크루스칼 알고리즘을 구현한 예제 코드입니다.

import sys
import heapq

# 분리 집합 클래스
class DisjointSet:
    def __init__(self):
        self.parent = None

# 분리 집합 합집합 연산
def unionset(set1, set2):
    set2 = findset(set2)
    set2.parent = set1

# 분리 집합 부모 찾기
def findset(set):
    while set.parent != None:
        set = set.parent

    return set

def kruskal(graphs, weights):
    mst_graphs = [ [ 0 for _ in range(len(graphs)) ] for _ in range(len(graphs)) ] # 최소 신장 트리
    vertex_sets = [ DisjointSet() for _ in range(len(graphs))] # 분리 집합 배열
    visited = set() # 방문 정보
    heap = [] # 최소 힙

    for vertex in range(len(graphs)):
        for target in range(vertex, len(graphs)):
            if weights[vertex][target] > 0:
                heapq.heappush(heap, (weights[vertex][target], vertex, target)) # (가중치, 정점1, 정점2) 쌍으로 힙에 저장

    weight_sum = 0

    while len(heap) > 0:
        pop = heapq.heappop(heap)
        w = pop[0]
        v1 = pop[1]
        v2 = pop[2]
        set1 = vertex_sets[v1]
        set2 = vertex_sets[v2]
        print('{}-{}: {}'.format(v1, v2, w))

        if findset(set1) != findset(set2): # 같은 집합이 아닐 경우
            unionset(set1, set2)
            # 최소 신장 트리 생성
            mst_graphs[v1][v2] = 1
            mst_graphs[v2][v1] = 1
            weight_sum += weights[v1][v2]

    # 출력용
    print("최소 가중치 합: ", weight_sum)
    for row in mst_graphs:
        print(row)

    return mst_graphs

if __name__ == "__main__":
    graphs = [
        [0, 1, 0, 0, 0, 1, 0],
        [1, 0, 1, 0, 0, 0, 1],
        [0, 1, 0, 1, 0, 0, 0],
        [0, 0, 1, 0, 1, 0, 1],
        [0, 0, 0, 1, 0, 1, 1],
        [1, 0, 0, 0, 1, 0, 0],
        [0, 1, 0, 1, 1, 0, 0]
        ]
    weights = [
        [0, 8, 0, 0, 0, 15, 0],
        [8, 0, 17, 0, 0, 0, 10],
        [0, 17, 0, 27, 0, 0, 0],
        [0, 0, 27, 0, 29, 0, 25],
        [0, 0, 0, 29, 0, 21, 23],
        [15, 0, 0, 0, 21, 0, 0],
        [0, 10, 0, 25, 23, 0, 0]
        ]

    mst_graphs = kruskal(graphs, weights)

0-1: 8
1-6: 10
0-5: 15
1-2: 17
4-5: 21
4-6: 23
3-6: 25
2-3: 27
3-4: 29
최소 가중치 합:  96
[0, 1, 0, 0, 0, 1, 0]
[1, 0, 1, 0, 0, 0, 1]
[0, 1, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 1]
[0, 0, 0, 0, 0, 1, 0]
[1, 0, 0, 0, 1, 0, 0]
[0, 1, 0, 1, 0, 0, 0]