[알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm)

다익스트라 알고리즘(Dijkstra Algorithm)

다익스트라 알고리즘은 그래프에서 정점 사이의 최단 경로를 찾는 알고리즘 입니다. 프림 알고리즘과 동작방식이 비슷하지만 다익스트라 알고리즘은 시작 정점에서 정점 V 까지의 경로의 길이를 기준으로 최단 경로를 연결합니다. (단 가중치가 음수인 경우 사용할 수 없습니다.)

다익스트라 알고리즘은 다음과 같은 원리로 동작합니다.

1. 시작 정점으로부터 각 정점까지의 경로의 길이를 저장할 배열을 만들고 모든 정점을 ∞(무한대)으로 초기화
2. 시작 정점의 경로의 길이를 0으로 초기화하고 시작 정점을 최단 경로에 추가
3. 최단 경로에 추가된 정점의 인접한 정점을 확인해서 경로의 길이를 갱신하고 최단 경로에 추가. (단 추가하려는 정점이 이미 최단 경로 안에 존재할 경우 경로의 길이가 갱신되기 이전의 경로보다 작다면 기존 경로를 폐기하고 현재 정점을 경유하도록 수정)
4. 모든 정점이 최단 경로에 추가될 때까지 3번 반복

이해를 돕기 위해 예를 들어 보겠습니다.

위 그래프에서 정점 1을 시작 정점으로 하겠습니다. 정점 1로부터 각 정점까지의 경로 길이를 저장할 배열을 선언하고 경로 길이를 ∞(무한대)으로 초기화 합니다. 시작 정점의 경로 길이는 0으로 초기화 합니다. 정점 1과 인접한 정점 0, 2, 6의 가중치를 확인해서 배열에 있는 경로 길이보다 작다면 경로 길이를 갱신하고 최단 경로에 추가합니다. 간선 1-0의 가중치는 8입니다. 가중치 8은 배열에 있는 경로 길이 ∞보다 작으므로 0의 경로 길이를 8로 갱신합니다. 2, 6도 같은 방법으로 경로 길이를 갱신합니다.

0과 인접한 정점은 5가 유일하므로 1-0-5까지의 경로 길이를 23(8+15)으로 갱신하고 최단 경로에 추가합니다.

2도 인접한 정점은 3이 유일하므로 같은 방법으로 경로의 길이를 44(17+27)으로 갱신하고 최단 경로에 추가합니다.

6과 인접한 정점 4, 3에서 1-6-4까지의 경로 길이는 33(10+23)으로 갱신하고 최단 경로에 추가합니다.

여기서 1-6-3까지의 경로 길이 35(10+25)는 기존 경로 1-2-3까지의 44(17+27)보다 작으므로 경로 길이를 갱신 및 기존 경로를 폐기하고 최단 경로에 추가합니다.

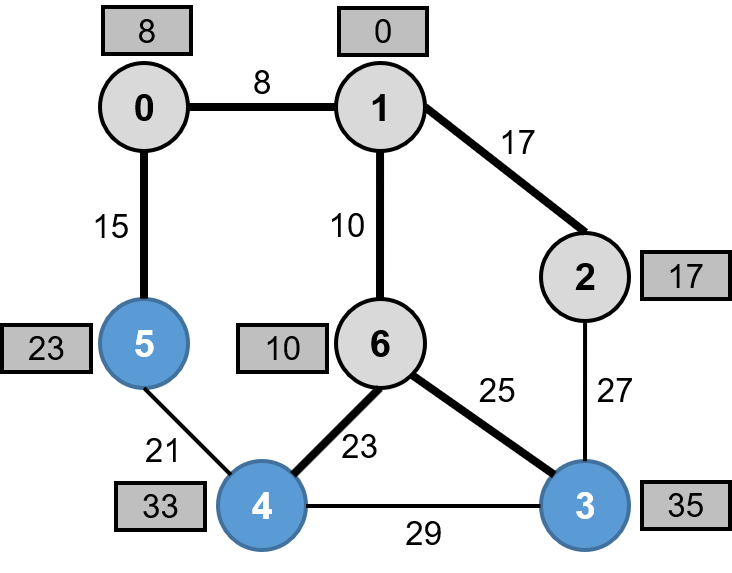
5와 인접한 정점은 4가 유일하고 1-0-5-4까지의 경로 길이 44(8+15+21)는 기존 경로 33보다 크므로 경로 길이를 갱신하지 않습니다.

4와 인접한 정점 5, 3은 모두 기존 경로 길이보다 커지므로 경로 길이를 갱신하지 않습니다.

3과 인접한 정점 4, 6도 마찬가지이므로 경로 길이를 갱신하지 않습니다.

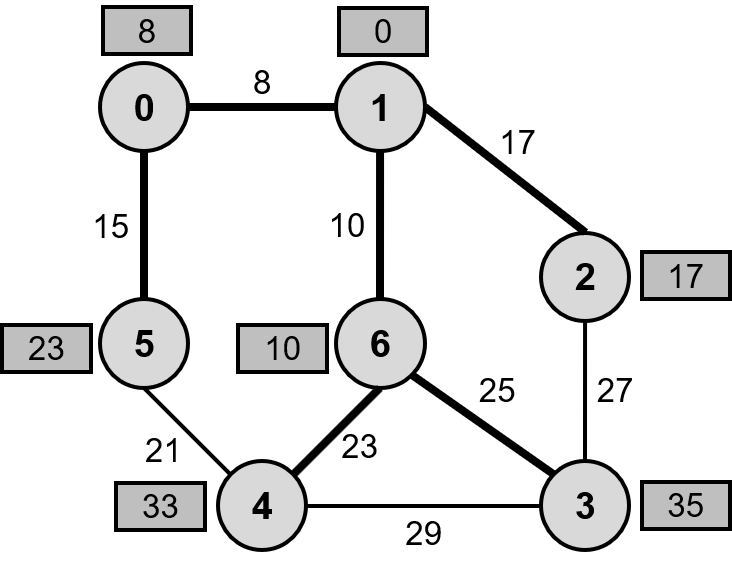
이제 더 이상 탐색할 정점이 없으므로 최단 경로 탐색을 종료합니다.

다익스트라 알고리즘 구현

다익스트라 알고리즘의 구현은 프림 알고리즘과 비슷합니다. 정점과 인접한 간선을 (가중치, 정점)으로 힙에 삽입하고, 힙에서 꺼낸 정점까지 경로 길이가 배열에 있는 기존 경로보다 작다면 경로 길이를 갱신하고 최단경로에 추가합니다. 이 과정을 힙이 비어 있을 때까지 반복하면 됩니다.

예제 코드에서는 최단 경로 그래프를 반환하도록 하였습니다. 다음은 다익스트라 알고리즘을 구현한 예제 코드입니다.

import sys
import heapq
import math

def dijkstra(start, graphs, weights):
    shortest_path = [ [ 0 for _ in range(len(graphs)) ] for _ in range(len(graphs)) ] # 최단 경로 그래프
    shortest_vertices = [-1 for _ in range(len(graphs))] # 최단 경로 연결 정보 (-1로 초기화)
    shortest_weights = [ math.inf for _ in range(len(graphs)) ] # 최단 경로 가중치 정보 (무한대 값으로 초기화)
    visited = set() # 방문 정보
    heap = [] # 최소 힙

    heapq.heappush(heap, (0, start)) # (가중치, 정점) 쌍으로 힙에 저장
    shortest_weights[start] = 0 # 시작 정점 경로 길이 0으로 초기화

    while len(heap) > 0:
        pop = heapq.heappop(heap)
        weight = pop[0]
        vertex = pop[1]
        visited.add(vertex)

        for target, value in enumerate(graphs[vertex]): # 인접한 간선 순회
            if target in visited:
                continue

            if value == 1 and shortest_weights[vertex] + weights[vertex][target] < shortest_weights[target]:
                heapq.heappush(heap, (weights[vertex][target], target))
                shortest_weights[target] = shortest_weights[vertex] + weights[vertex][target]
                shortest_vertices[target] = vertex

    # 최단 경로 그래프 생성
    for a, b in enumerate(shortest_vertices):
        if b >= 0:
            shortest_path[a][b] = 1
            shortest_path[b][a] = 1

    # 출력용
    for row in shortest_path:
        print(row)

    return shortest_path


if __name__ == "__main__":
    graphs = [
        [0, 1, 0, 0, 0, 1, 0],
        [1, 0, 1, 0, 0, 0, 1],
        [0, 1, 0, 1, 0, 0, 0],
        [0, 0, 1, 0, 1, 0, 1],
        [0, 0, 0, 1, 0, 1, 1],
        [1, 0, 0, 0, 1, 0, 0],
        [0, 1, 0, 1, 1, 0, 0],
        ]
    weights = [
        [0, 8, 0, 0, 0, 15, 0],
        [8, 0, 17, 0, 0, 0, 10],
        [0, 17, 0, 27, 0, 0, 0],
        [0, 0, 27, 0, 29, 0, 25],
        [0, 0, 0, 29, 0, 21, 23],
        [15, 0, 0, 0, 21, 0, 0],
        [0, 10, 0, 25, 23, 0, 0],
        ]

    shortest_path = dijkstra(1, graphs, weights)

[0, 1, 0, 0, 0, 1, 0]
[1, 0, 1, 0, 0, 0, 1]
[0, 1, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 1]
[0, 0, 0, 0, 0, 0, 1]
[1, 0, 0, 0, 0, 0, 0]
[0, 1, 0, 1, 1, 0, 0]